- Según la definición de derivada:
- lo que es
- Entonces, usando la fórmula del seno de la suma de dos ángulos, se tiene que
- Factorizando
- Separando, dado que todas las funciones son continuas, se tiene
- Como:
 esto es así ya que
esto es así ya que 
- reemplazando para θ = h y ϕ = 0
- Se tiene que:

- y utilizando el límite conocido:

- Se obtiene que el primer término es 0, entonces
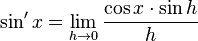
- Como:
- Por ello puede simplificarse, y se tiene que




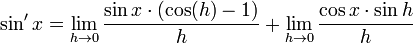

No hay comentarios:
Publicar un comentario